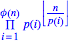| Fri, 14 Jun 2013
MathML browser extensionsIt's really annoying that there still isn't universal support for MathML. Things have got better recently though, with Safari finally supporting it. Of the major browsers, though, there are still two that don't. First, IE. It doesn't matter. It is only used for three things: first, to download a browser that doesn't suck; second, if it is chosen by someone who is stupid, ignorant or malicious; third, by people who need to compare browsers. Second, Chrome. Despite its lack of MathML, Chrome is IMO the best browser out there. It works on multiple platforms, has lots of extensions available, and has very good support for synchronising things like bookmarks and open pages across devices. And now there's a plugin for it to support MathML! And of course Chrome supports it without a plugin on iOS, because it uses the Safari rendering engine there. update: Safari on the desktop still doesn't render it particularly well, despite it working just fine on my phone. Huzzah! | ||
| Wed, 16 Jan 2013
Lewis Carroll in Numberland, by Robin Wilson
To most people, Lewis Carroll is nothing but an author of childrens' books and a photographer of ill repute. Nothing could be further from the truth. He was also Charles Lutwidge Dodgson, an eminent mathematician at Oxford, with most of his work being in geometry and matrix algebra. He spent much of his time teaching undergraduates, but also children in various schools around Oxford and private pupils, and published at least as much serious work as he did fiction and nonsense. It is said that after Queen Victoria read "Alice's Adventures in Wonderland", she was so charmed that she demanded that she be sent a copy of his next book. And duly, she received "An Elementary Treatise on Determinants, With Their Application to Simultaneous Linear Equations and Algebraic Equations" and was not amused. Much of his mathematical work, being pedagogical, is now out of date and sometimes even wrong. For example, much of his energy was spent on teaching Euclid to undergraduates, material that is these days covered at A-level in a completely different way, and he was so opposed to the study of non-Euclidean geometries as to waste time writing against them. But that doesn't detract from the fact that he was a great teacher of mathematics, to students at all levels from young children to the most learnèd. Of his works that are still relevant, his two-part "Symbolic Logic" appears (from its description in this short biography) to be worth looking at, for his method of figuring out syllogisms through diagrams, and how he expanded his diagrams to deal with showing the interactions of any number of sets, where Venn diagrams break down at six sets. In 1884 he published what is now an obscure work on psephology, "The Principles of Parliamentary Representation" in which he considers what it means for an election to be fair, and methods to achieve this in reality. I'm very pleased to say that he comes to the same conclusion that I did: large multi-member constituencies with some form of proportional representation within each constituency. And related to this, and driven by his interest in tennis, he analysed whether the traditional knockout style of tournament was a good way of ranking players by ability (it isn't: consider what happens if the best and second-best players meet in the first round) and published under his Carroll pen-name a pamphlet with the delightful title of "Lawn Tennis Tournaments: The True Method of Assigning Prizes with a Proof of the Fallacy of the Present Method" whose recommendations have not, unfortunately, been taken up. It is an interesting "what-if" to imagine whether they would have been if he had published it under the name of Dodgson and the effect this would have on knock-out tournaments in all manner of sports. I would have liked to see a bit more space given in this biography to all three of those subjects, even bearing in mind that a biography is a book about the man, not about the details of his work. After all, if the author could fit in so much material about puns and mathematical games, he could surely fit in a bit more about those works of Dodgson's that are the most relevant today. I wonder if, perhaps, Wilson was concerned that that would make the book "too technical". If that's the reason, then Shame, Shame! For those with an interest in mathematics (at any level, from schoolchild to professional), this book is very much worth reading and worth buying. For general readers I hesitate to recommend purchasing it except to Carroll's most ardent fans. | ||
| Wed, 6 Jul 2011
Star ratings re-revisitedI did, very briefly, consider a completely different rating system for my reviews, instead of just awarding 0 to 5 shiny gold stars. I considered rating books out of ten on several axes - for example, entertainment, literary merit, imagination, consistency. I would then combine them by treating those scores as the co-ordinates of a point in an N-dimensional space, the overall rating being the distance of that point from the origin, or equivalently, they are components of a velocity vector in an N-dimensional space. Let me give a couple of examples: The Quantum Thief might score 8/10 for entertainment, 10/10 for literary merit, 9/10 for imagination, and 10/10 for consistency. The score, then, is sqrt(82+102+92+102) = 18.6. A perfect score on those axes would be sqrt(4*102) = 20. So to normalise to a score out of ten we divide by 2, giving 9.3/10. I actually gave it 5/5. A Mighty Fortress, on the other hand, might get 5/10 for entertainment, 2/10 for literary merit, 2/10 for imagination, and 8/10 for consistency, for a score of 9.8, which normalises to 4.9/10. I actually gave it 2/5. There are at least three obvious reasons why I didn't go with this.
| ||
| Fri, 10 Sep 2010
Webkit and ASCIIMathMLAs you will no doubt know by now, I occasionally perpetrate mathematics. But it sucks to have to say in something like this "take the product of p(i)int(n/p(i)) for i=1 to i=Φ(n)". It would be much better if I could embed a proper formula. There's a standard way of doing this, called MathML, and it's fucking horrible. And in any case, browser support for MathML is piss-poor. However, it's getting better - Firefox now supports it fairly well, and Webkit does too, although not quite as well as Firefox. There are also a few useful tools for making MathML suck less, in particular ASCIIMathML, which I am now using. Using that, I type the above equation thus: \prod_(i=1)^(\phi(n))p(i)^(\lfloorn/(p(i))\rfloor) and it renders thus in your browser: `\prod_(i=1)^(\phi(n))p(i)^(\lfloorn/(p(i))\rfloor)` it should render something like this: Note that at the time of writing, Webkit doesn't properly render the floor(n/p(i)) as a superscript to p(i). Even with the flaws in common browsers (and the complete lack of support in many, including Safari) I'm going to start using it, because it's just so damned useful. Webkit and Firefox support it, which is good enough for me, and because Webkit is really just the nightly builds of Safari, we can expect a near-future release of Safari to support it too. Incidentally, this journal entry exposes a bug in ASCIIMathML as well as in the current Webkit - can you spot it? Update: it took the author of ASCIIMathML mere hours to respond to my bug report with a fix. Makes me rather ashamed of some of the bugs that have been mouldering in my RT queue for over a year :-) | ||
| Sat, 3 Oct 2009
Graphing tool
Update: now 48.3% even shinier - see on the right | ||
| Wed, 30 Sep 2009
Optimising n! - revisited againFor the background, see this post and this post. I have had An Branewave! When I said that 100! = 250 * 333 * 520 * 714 * 119 * ... was wrong (which it is) I stupidly didn't realise that there is a pattern to the missing terms. The 250 comes from observing that there a 50 multiples of 2 less than or equal to 100. There are also 25 multiples of 4 (also known as 22), 12 multiples of 8 (aka 23), 6 multiples of 24, 3 multiples of 25, and 1 of 26. the 25 multiples of 4 contribute another 225. The 12 multiples of 8 (which of course are also multiples of 4) contribute another 212, and so on. So we see that 100! is divisible by 250 + 25 + 12 + 6 + 3 + 1, or 297. There is, of course, a similar pattern for all the other prime factors. | ||
| Fri, 25 Sep 2009
Combining functionsThere was a great programme on Radio 4 yesterday about Newton and Leibnitz. I'm not sure why, but it inspired me to consider the curve that is constructed from It can obviously be done. Consider that to fit a curve to any* three points, you can do it with a curve I'm sure that this can be done - obviously you can't actually calculate an infinite number of constants, but I'm sure that with a bit of integration it could be done. And it can be done for any such pair of functions which meet at a point. However, on further reflection I'm not entirely convinced that it can be done in the general case - you have that pesky discontinuous yes/no conditional in the middle: "is x <= n?". * not strictly true - consider (0,0), (0,1), (1,0). | ||
| Tue, 28 Apr 2009
Factoring FactorialsTake a factorial. Any factorial. Factor it*. Notice a Pattern. That pattern is that if you list all of the prime factors in order and the number of times they appear, at no point does any larger factor appear more often than any smaller factor. This would appear to be obvious, and it "obviously" applies to all factorials** (I've verified it by hand up to 28!, at which point I got bored). But I'm finding it hard to put a proof into words - or more concisely but equivalently - into symbols. * this is easy. While factoring 1124000727777607680000 might be quite hard, if you know that it's 22! it becomes trivial because we know that it is divisible by 2, 3, 4, 5, ..., 21, 22, each of which is trivially factorable. Given that each number is the product of a unique set*** of factors, the factors of 22! can only be the set of all the factors of all the numbers we multipled to get 22!. Easy! ** it becomes obvious when you consider Eratosthenes' method for testing primality. *** yes, I know, it's not really a set. | ||
| Mon, 10 Nov 2008
UmbrellasWhat's the point of umbrellas? To be effective, their diameter needs to be slightly more than Given that rain can subtend any angle from 0 to 90° from the vertical, then unless you wish to be your umbrella supplier's very best friend in the whole world, you need a Very Large umbrella. And yet, no-one carries such a thing. Indeed, I don't think anyone makes such a thing suitable for anyone other than midgets. So we see that every umbrella user has, from the point of view of keeping themselves dry, made the wrong decision. Their partial solutions are no better than what they would achieve by wearing a good coat and a hat. Unfortunately, their partial solutions come at the cost to everyone else of getting poked in the face by the metal spikes at the edge of the umbrella. * the value of "slightly more" is a function of ϑ and the shape of the human body. A good approximation would be to assume that a person's width is h/3 and their depth is h/4. | ||
| Wed, 27 Aug 2008
Optimising n! - revisitedFor the background, see this post. Late one night I thought that you might be able to simplify n-factorial thus: `\prod_(i=1)^(\phi(n))p(i)^(\lfloorn/(p(i))\rfloor)` Where:
Now, without using a lookup table, p() and Φ() are hard to calculate, but at least you'd avoid a lot of the problems that come from using the stupendously big numbers that come as intermediate results in calculating factorials. Unfortunately, that formula is wrong anyway. It's a restatement of this: 100! = 250 * 333 * 520 * 714 * 119 * ... which came from noticing that 100! is the product of 50 numbers which have 2 as a prime factor, 33 numbers which have 3 as a prime factor, 20 numbers that have 5 as a prime factor, and so on. Unfortunately, it doesn't take account of numbers like 4 and 18 which have a repeated prime factor - 4, for example, is 2 * 2 and 18 is 2 * 3 * 3. Bother. | ||
| Tue, 22 Jul 2008
Wikipedia: WRONG AGAINWikipedia has a reputation for being of rather low quality, particularly in the humanities. In the sciences and technology it is supposed to be pretty good. But today, I found an error in their article about ... the triangle. One of the most basic mathematical concepts. And they got it wrong. Joy. OK, to be fair, it's only subtlely wrong, is correct for the majority of cases, and one could argue that the context in which the inaccurate information is presented makes it OK. But I disagree. In a section called "Basic facts" they first mention that triangles were described thoroughly by Euclid. Good. In the next paragraph, they say that the internal angles add up to 180°. Not so good. They only do so in some spaces, the most commonly known of which is the Euclidean space. Anyway [click click click type click] I've fixed it now. I wonder how long it'll stay fixed, or whether some wanker will revert my pedantry. | ||
| Wed, 11 Jun 2008
Optimising n!If you want to add up all the numbers from 1 to n, you can do it two ways. The slow, inefficient way is to calculate: 1 + 2 + 3 + ... + n The quick way is to remember what you were taught in school, that: 1 + 2 + 3 + 4 + 5 + 6 = (6 + 1) + (2 + 5) + (3 + 4) = 7 + 7 + 7 and that in general: 1 + 2 + ... + n = n(n+1)/2 This optimisation might not matter for small values of n, but for n = 1000000 it really makes a big difference. This got me thinking whether there was a similar trick for calculating the product of all numbers from 1 to n - that is, n-factorial, or n!. This matters even more for n! because it gets so large so quickly that computers are unable to accurately represent the intermediate values. In fact, 20! is the largest that can be respresented on a 64 bit machine. 21! can only be approximated, as you need to use a floating point number. This means that not only is calculating really big factorials time-consuming, it's not possible at all to do it accurately with native datatypes. I don't even know if there is a simple re-statement of n! like there is for the sum above, but I'm gonna spend a few idle minutes working on it. | ||